Công thức chung hoàn tác mọi chuyển động quay phức tạp của vật thể

Hãy tưởng tượng quay một ngọn và sau đó để nó nghỉ ngơi. Có cách nào để bạn quay lại đỉnh để nó kết thúc ở vị trí chính xác mà nó bắt đầu, như thể bạn chưa bao giờ quay nó chút nào không? Đáng ngạc nhiên, vâng, các nhà toán học đã phát hiện ra một công thức phổ quát để hoàn tác chuyển động quay của gần như bất kỳ vật thể nào.

Theo trực giác, có cảm giác như cách duy nhất để hoàn tác một chuỗi vòng quay phức tạp là cẩn thận thực hiện từng chuyển động ngược lại chính xác một. Nhưng [Jean-Pierre Eckmann] tại Đại học Geneva và [Tsvi Tlusty] tại Viện Khoa học và Công nghệ Quốc gia Ulsan đã tìm thấy một nút đặt lại ẩn liên quan đến việc thay đổi kích thước của vòng quay ban đầu bằng một hệ số chung, một quá trình được gọi là tỷ lệ và lặp lại nó hai lần.

Trong trường hợp quay đầu, nếu vòng quay ban đầu của bạn đã xoay đỉnh ba phần tư, bạn có thể quay lại điểm bắt đầu bằng cách chia tỷ lệ vòng quay của mình lên một phần tám, sau đó lặp lại hai lần để cung cấp cho bạn thêm một phần tư vòng quay. Nhưng Eckmann và Tlusty đã cho thấy cũng có thể làm điều này cho các tình huống phức tạp hơn nhiều.

"Nó thực sự là một thuộc tính của hầu hết mọi vật thể quay, như một vòng quay hoặc một qubit hoặc một con quay hồi chuyển hoặc một cánh tay robot", Tlusty nói. "Nếu các vật thể đi qua một con đường rất phức tạp trong không gian, chỉ bằng cách chia tỷ lệ tất cả các góc quay theo cùng một hệ số và lặp lại quỹ đạo phức tạp này hai lần, chúng sẽ quay trở lại ban đầu."

Chứng minh toán học của họ bắt đầu với một danh mục tất cả các vòng quay có thể có trong ba chiều không gian. Danh mục này, được gọi là SO(3), có thể được mô tả bằng cách sử dụng một không gian toán học trừu tượng có các quy tắc đặc biệt và có cấu trúc giống như một quả bóng, với hành động đẩy một vật thể qua một chuỗi các vòng quay trong không gian thực tương ứng với việc di chuyển từ điểm này sang điểm khác trong quả bóng.

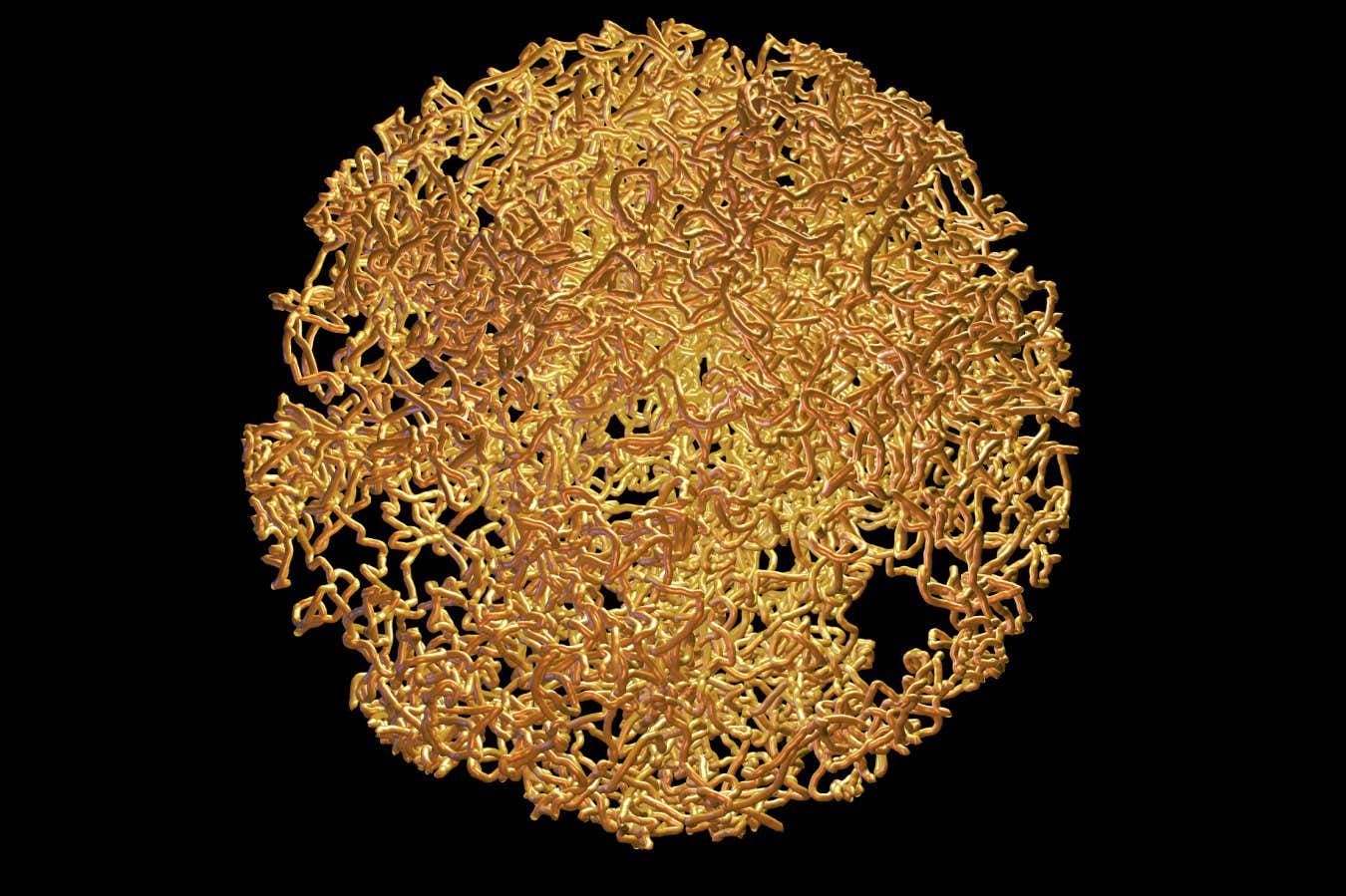
Một số đường dẫn có thể được thực hiện qua không gian toán học SO (3), tương ứng với chuỗi quay trong không gian thực

Tsvi Tlusty

Những gì Eckmann và Tlusty nhận ra là, do kết quả của cách SO(3) được cấu trúc, việc hoàn tác một vòng quay nửa chừng tương đương với việc tìm ra một đường dẫn sẽ hạ cánh bạn ở bất kỳ đâu trên bề mặt của quả bóng. Điều này dễ dàng hơn nhiều so với việc cố gắng đến trung tâm, bởi vì bề mặt được tạo thành từ nhiều điểm, Tlusty nói.

Cặp đôi đã dành rất nhiều thời gian để theo đuổi những căng thẳng của lý luận toán học mà không dẫn đến đâu, Eckmann nói. Cuối cùng, những gì hiệu quả là một công thức thế kỷ 19 để kết hợp hai vòng quay tiếp theo được gọi là công thức Rodrigues và một định lý năm 1889 từ một nhánh toán học được gọi là lý thuyết số. Cuối cùng, các nhà nghiên cứu kết luận rằng hệ số mở rộng cần thiết cho việc thiết lập lại của chúng gần như luôn tồn tại.

Đối với Eckmann, công trình mới là một minh chứng cho thấy toán học có thể phong phú như thế nào ngay cả trong một lĩnh vực được nghiên cứu về vòng quay. Tlusty nói rằng nó cũng có thể có những hậu quả thực tế, ví dụ, trong cộng hưởng từ hạt nhân (NMR), là cơ sở của chụp cộng hưởng từ (MRI). Bằng chứng mới có thể giúp phát triển các quy trình để hoàn tác các vòng quay không mong muốn có thể cản trở quá trình chụp ảnh.

Công việc này cũng có thể dẫn đến những tiến bộ trong robot, Josie Hughes tại Trường Bách khoa Liên bang Lausanne cho biết. Ví dụ, một robot lăn có thể được tạo ra để đi theo một con đường lặp lại các phân đoạn, bao gồm một chuyển động cuộn-đặt lại-cuộn đáng tin cậy, về lý thuyết, có thể kéo dài mãi mãi. "Hãy tưởng tượng nếu chúng ta có một robot có thể biến đổi giữa bất kỳ hình dạng cơ thể rắn nào, thì nó có thể đi theo bất kỳ con đường mong muốn nào chỉ đơn giản thông qua việc biến đổi hình dạng", cô nói.

Trong bối cảnh Việt Nam, phát hiện về nút đặt lại cho chuyển động quay có thể mở ra cơ hội ứng dụng đa dạng. Trong lĩnh vực y tế, kỹ thuật MRI và NMR tại các bệnh viện tuyến trung ương như Bạch Mai hay Chợ Rẫy có thể nâng cao chất lượng hình ảnh và rút ngắn thời gian chụp nhờ quy tắc hoàn tác vòng quay. Về chế tạo robot, các viện nghiên cứu công nghệ như Viện Công nghệ Việt Nam hay các startup robot trong các khu công nghệ cao có thể áp dụng công thức này để tối ưu chuyển động cho robot di động, robot phẫu thuật hoặc robot sản xuất. Hơn nữa, nền tảng toán học SO(3) còn có thể được đưa vào chương trình giảng dạy tại các trường đại học kỹ thuật như Bách Khoa TP.HCM, giúp sinh viên tiếp cận sớm với các công cụ lý thuyết hiện đại. Sự kết hợp giữa nghiên cứu cơ bản và ứng dụng thực tiễn sẽ góp phần phát triển mạnh mẽ ngành khoa học công nghệ ở Việt Nam.